Exercícios de física - APLICAÇÕES DA LEIS DE NEWTON
01-(UNIFESP-SP)

Suponha que um comerciante inescrupuloso aumente o valor
assinalado pela sua balança, empurrando sorrateiramente o prato para baixo com
uma força de módulo F=5,0 N, na direção e sentido indicados na figura.
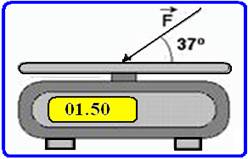
Com essa prática, ele consegue fazer com que uma mercadoria
de massa 1,5 kg seja medida por essa balança como se tivesse massa de:
considere g=10m/s2 e sen37o=0,6
a) 3,0 kg.
b) 2,4 kg. c)
2,1 kg. d)
1,8 kg.
e) 1,7 kg.
02(UFPE-PE)

Um bloco A, de massa igual a 2,0 kg, é colocado sobre um bloco B, de massa igual 4,0 kg, como mostrado na figura.
Sabendo-se que o sistema permanece em repouso sobre
uma mesa, calcule a força que a mesa exerce sobre o bloco B, em newtons.
03-(UFSCAR-SP)

O joão-teimoso é um boneco que, deslocado de sua posição de
equilíbrio, sempre volta a ficar em pé. Suponha que uma

criança segure um joão-teimoso na posição da figura e logo
em seguida o solte, sobre uma superfície horizontal. Assinale a alternativa que
melhor representa o esquema das forças que, com exceção das forças de atrito,
atuam sobre o joão-teimoso deitado, imediatamente após ser solto pela criança.

04-(UFRJ-RJ)

Uma pessoa idosa, de 68kg, pesa-se com sua bengala apoiada
no chão, ao lado da balança, como mostra a figura.

Com a pessoa em repouso a leitura da balança é 650N.
Considere g=10m/s2.
a) Supondo que a força exercida pela bengala sobre a pessoa
seja vertical, calcule o seu módulo e determine o seu sentido.
b) Calcule o módulo da força que a balança exerce sobre a
pessoa e determine a sua direção e o seu sentido.
05-(FUVEST-SP)

Uma força de 1newton (1N) tem a ordem de grandeza do peso
de:

a) um homem adulto
b) uma criança recém-nascida
c) um litro de leite
d) uma xicrinha cheia de café
e) uma moeda
06-(FGV-SP)

Durante a cerimônia de formatura, o professor de física,
teve seu pensamento absorvido pela pilha de duas camadas de

estojos de diplomas, todos iguais, escorada de ambos os
lados, por um copo contendo água.
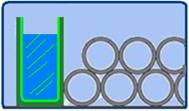
O professor lembrava que sen 30o=cos 60o=1/2
e que sen 60o=cos 30o=√3/2. Admitindo que cada
estojo tivesse o mesmo peso de módulo P, determinou mentalmente a intensidade
da força de contato exercida por um estojo da fila superior sobre um da fila
inferior, força que, escrita em termos de P, é
a)
(√3/6)P
b)
(√3/3)P
c)
(√3)P
d) P/4
e) P/2
07-(UEG-GO)

Entre os poucos animais que desenvolveram o “pára-quedismo”
está o sapo voador de Bornéu – Rhacophorus dulitensis, apresentado na figura a
seguir.
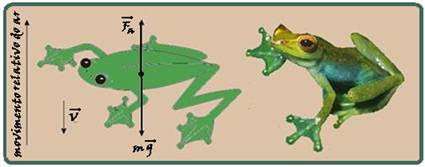
Na ilustração, 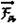 e
e  são, respectivamente, a força de
resistência do ar e a força peso.
são, respectivamente, a força de
resistência do ar e a força peso.
Considerando que esse animal tenha se atirado do alto de uma
árvore em direção ao solo, o seu pára-quedas será utilizado e, durante sua
queda,
a) as suas membranas interdigitais nas patas favorecem o
aumento da força de resistência do ar, haja vista que elas aumentam a área de
contato com o ar.
b) a resultante das forças que atuam sobre ele tenderá a se
tornar nula, levando-o, necessariamente, ao repouso no ar.
c) a sua velocidade tenderá a um valor limite, chamada de
velocidade terminal, independentemente da resistência do ar.
d) a sua aceleração será nula em todo o percurso,
independentemente da resistência do ar.
08-(UFABC)

Um mecânico afirma ao seu assistente que é possível erguer e
manter um carro no alto e em equilíbrio estático, usando-se um contrapeso mais
leve do que o carro. A figura mostra, fora de escala, o esquema sugerido pelo
mecânico para obter o seu intento.
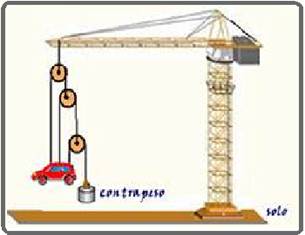
Considerando as polias e os cabos como ideais e, ainda, os
cabos convenientemente presos ao carro para que não haja movimento de rotação,
determine a massa mínima do contrapeso e o valor da força que o cabo central
exerce sobre o carro, com massa de 700 kg, quando esse se encontra suspenso e em equilíbrio estático.
09-(UNIMONTES-MG)

Um macaco de 10kg sobe por uma corda de massa desprezível,
que passa sobre o galho de uma árvore (veja a figura).
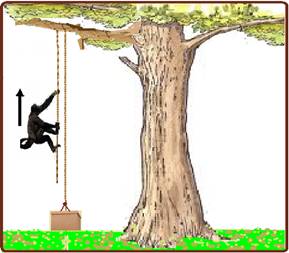
A corda pode deslizar, sem atrito, sobre a superfície do
galho. A outra extremidade da corda está presa a uma caixa cuja
massa é 15 kg. O menor valor do módulo da aceleração que o
macaco deve ter ao subir pela corda, para erguer a caixa, é igual a: Dado: g =
9,8 m/s2.
a) 9,8 m/s2 b) 2,4 m/s2 c)
7,3 m/s2 d) 4,9 m/s2
e) zero
10-(ITA-SP)

Uma pilha de seis blocos iguais, de mesma massa m, repousa
sobre o piso de um elevador, como mostra a figura.
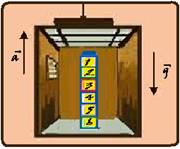
O elevador está subindo em movimento uniformemente retardado
com aceleração de módulo a. O módulo da força que o bloco 3 exerce sobre o
bloco 2 é dado por:
a) 3m(g + a) b)
3m(g – a) c) 2m(g +
a) d) 2m(g –
a) e) m(2g – a)
11-(PUC-MG)

Muitos carros e transportes modernos estão equipados com um
sistema de frenagem intitulado ABS, que evita que o

pneu deslize quando os freios forem acionados. O sistema
funciona através de um sensor que verifica, dezenas de vezes por segundo, se a
roda “travou”, ou seja, parou de girar. Se isso ocorrer, ele momentaneamente
libera aquela roda da ação do freio, para só voltar a aplicá-lo quando a roda retomar
seu movimento normal de rotação.
Esse sistema garante frenagens mais seguras, e em espaço
menor, porque:
a) quando a roda “trava”, há uma perda de energia
mecânica do sistema que deve ser evitada.
b) quando a roda “trava”, há um superaquecimento do sistema
de freios que deve ser evitado.
c) a inércia do carro é maior com a roda “travada” do
que com a roda girando.
d) a dirigibilidade do carro é maior com a roda
“travada” do que com a roda girando.
e) o coeficiente de atrito estático é maior que o coeficiente
de atrito cinético.
12-(PUC-RJ)

Uma locomotiva puxa uma série de vagões, a partir do
repouso.

Qual é a análise correta da situação?
a) A locomotiva pode mover o trem somente se for mais
pesada do que os vagões.
b) A força que a locomotiva exerce nos vagões é tão
intensa quanto a que os vagões exercem na locomotiva; no entanto, a força de
atrito na locomotiva é grande e é para frente, enquanto que a que ocorre nos
vagões é pequena e para trás.
c) O trem se move porque a locomotiva dá um rápido
puxão nos vagões, e, momentaneamente, esta força é maior do que a que os vagões
exercem na locomotiva.
d) O trem se move para frente porque a locomotiva puxa
os vagões para frente com uma força maior do que a força com a qual os vagões
puxam a locomotiva para trás.
e) Porque a ação é sempre igual à reação, a locomotiva
não consegue puxar os vagões.
13- (UFSCAR-SP)

O sistema esquematizado compõe-se de um elevador de massa M
e um homem de massa m. O elevador está suspenso por uma corda que passa por uma
polia fixa e vem às mãos do operador; a corda e a roldana são supostas ideais.
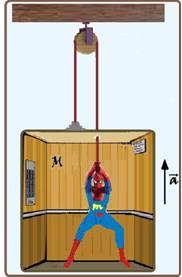
O operador puxa a corda e sobe com aceleração constante a,
juntamente com o elevador. São supostos conhecidos M, m, a e g. Determine a
intensidade da força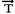 que traciona a corda.
que traciona a corda.
14-(UNESP-SP)

Uma barra AC homogênea de massa m e comprimento L, colocada
numa mesa lisa e horizontal, desliza sem girar sob ação de uma força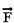 , também horizontal,
aplicada na sua extremidade esquerda.
, também horizontal,
aplicada na sua extremidade esquerda.
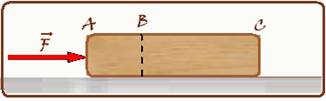
Mostre que a força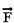 com que a fração BC de comprimento (2.L/3),
atua sobre a fração AB é igual a (- 2.
com que a fração BC de comprimento (2.L/3),
atua sobre a fração AB é igual a (- 2.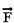 /3).
/3).
15-(PUC-RJ)

Alberto (A) desafiou seu colega Cabral (C) para uma
competição de cabo de guerra, de uma maneira especial, mostrada na figura.
Alberto segurou no pedaço de corda que passava ao redor da polia enquanto que
Cabral segurou no pedaço atado ao centro da polia. Apesar de mais forte, Cabral
não conseguiu puxar Alberto, que lentamente foi arrastando o seu adversário até
ganhar o jogo.

Sabendo que a força com que Alberto puxa a corda é de 200 N
e que a polia não tem massa nem atritos:
a) especifique a tensão na corda que Alberto está segurando;
b) desenhe as forças que agem sobre a polia, fazendo um
diagrama de corpo livre;
c) calcule a força exercida pelo Cabral sobre a corda que
ele puxava;
d) considerando que Cabral foi puxado por 2,0 m para frente, indique quanto Alberto andou para trás.
16-(UEL-PR)

Considere o sistema constituído por três blocos de massas m1,
m2 e m3, apoiados um sobre o outro, em repouso sobre
uma superfície horizontal, como mostra a figura a seguir.
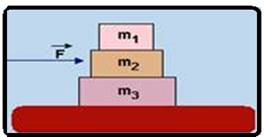
Observe que uma força 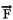 é aplicada ao bloco de massa m2,
conforme a representação. Entretanto, esta força é incapaz de vencer as forças
de fij entre os blocos mi e mj, onde
i e j variam de 1 a 3.
é aplicada ao bloco de massa m2,
conforme a representação. Entretanto, esta força é incapaz de vencer as forças
de fij entre os blocos mi e mj, onde
i e j variam de 1 a 3.
17-(UNESP-SP)

Um rebocador puxa duas barcaças pela águas de um lago
tranqüilo. A primeira delas tem massa de 30 toneladas e a segunda, 20
toneladas. Por uma questão de economia, o cabo de aço I que conecta o rebocador
à primeira barcaça suporta, no máximo, 6.105N, e o cabo II, 8.104N.

Desprezando o efeito de forças resistivas, calcule a
aceleração máxima do conjunto, a fim de evitar o rompimento de um dos cabos.
18-(FUVEST-SP)

Um sistema mecânico é formado por duas polias ideais que
suportam três corpos A, B e C de mesma massa m, suspensos por fios ideais como
representado na figura.
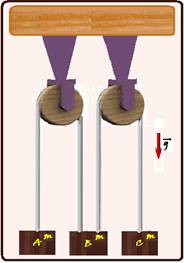
O corpo B está suspenso simultaneamente por dois fios,
um ligado a A e outro a C. Podemos afirmar que a aceleração do corpo B será:
a)
zero b) (g/3)
para baixo c)
(g/3) para
cima d)
(2g/3) para
baixo e)
(2g/3) para cima
19-(UERJ-RJ)

A figura abaixo representa o plano inclinado ABFE,
inserido
em um paralelepípedo retângulo ABCDEFGH de base horizontal, com 6 m de
altura CF, 8 m de comprimento BC e 15 m de largura AB, em repouso,
apoiado no solo.
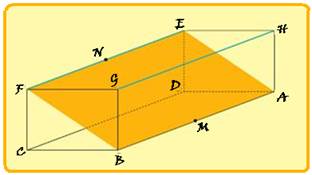
Considere o deslocamento em movimento retilíneo de um corpo
P1 de M até N e de um corpo P2 de A até F.
Admita as seguintes informações:
- P1 e P2 são corpos
idênticos;
- F1 e F2 são, respectivamente,
as componentes dos pesos de P1 e P2 ao longo
das respectivas trajetórias;
- M e N são, respectivamente, os pontos médios das arestas
AB e EF.
Considerando esses dados, a razão F1/F2 equivale
a:
a)
17/6
b) 4/3
c) √(15)/3
d) √(15)/3
e) √(13)/2
20-(UFG-GO)

No sistema representado na figura abaixo, as duas molas são
iguais, têm 1 m de comprimento e estão relaxadas. Quando o fio é cortado, a esfera
de massa 5,1 kg desce 1 m até parar momentaneamente.
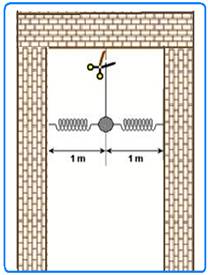
Dados: √2=1,41 e g=10m/s2. Calcule o valor
da constante elástica k das molas.
21-(FB)

A mola helicoidal (figura 1), de constante elástica k=12N/m,
foi partida em 3 partes iguais. Em seguida, essas 3 partes foram associadas em
paralelo (figura 2) e em série (figura 3).
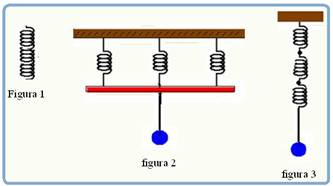
As massas das figuras 2 e 3 são iguais e valem 100g. Adote
g=10m/s2 e determine:
a) a constante elástica de cada parte.
b) o período de oscilação do conjunto quando as três molas
estão associadas em paralelo.
c) o período de oscilação do conjunto quando as três molas
estão associadas em série.
22-(UFRS-RS)

A figura a seguir representa seis pêndulos simples, que
estão oscilando num mesmo local.
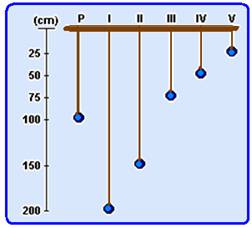
O pêndulo P executa uma oscilação completa em 2 s. Qual dos
outros pêndulos executa uma oscilação completa em
1 s?
a) I. b) II.
c) III. d) IV. e) V.
23-(ITA-SP)

Um pêndulo simples oscila com um período de 2s. Se cravarmos
um pino a uma distância 3L/4 do ponto de suspensão
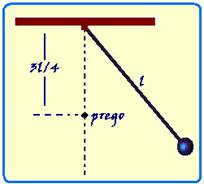
e na vertical que passa por aquele ponto, como mostrado na
figura, qual será o novo período do pêndulo?
24-(ITA-SP )

Dois pêndulos de comprimento L1 e L2
conforme a figura, oscilam de tal modo que os dois bulbos de encontram sempre
que são decorridos 6 períodos do pêndulo menor e 4 períodos do pêndulo maior. A
relação L2/L1 deve ser:
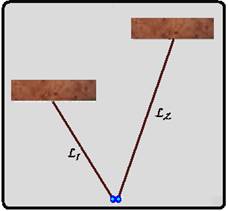
a) 9/4 b)
3/2 c) 2 d) 4/9
e) 2/5
25-(ITA-SP)

Um relógio tem um pêndulo de 35 cm de comprimento. Para regular seu funcionamento, ele possui uma porca de ajuste
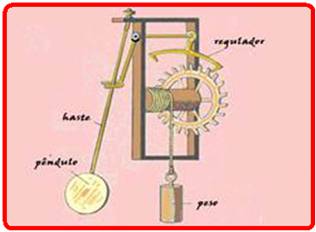
que encurta o comprimento do pendulo de 1 mm a cada
rotação completa à direita e alonga este comprimento de 1 mm a cada
rotação completa à esquerda.
Se o relógio atrasa um minuto por dia, indique o número
aproximado de rotações da porca e sua direção necessários para que ele funcione
corretamente.
a) 1 rotação à esquerda b) 1/2 rotação à
esquerda c) 1/2 rotação à direita d) 1 rotação à
direita e) 1 e 1/2 rotações à direita.
26-(UFJF-MG)

Um caminhão é carregado com duas caixas de madeira, de
massas iguais a 500kg, conforme mostra a figura.

O caminhão é então posto em movimento numa estrada reta e
plana, acelerando até adquirir uma velocidade de 108km/h e depois é freado até
parar, conforme mostra o gráfico. (g=10m/s2).
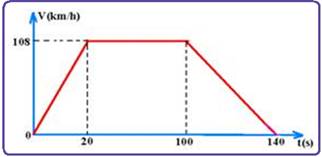
O coeficiente de atrito estático entre as caixas e a carroceria
do caminhão é μ=0,1. Qual das figuras abaixo melhor representa a
disposição das caixas sobre a carroceria no final do movimento?

27-(ENEM-MEC-012)

Os freios ABS são uma importante medida de segurança no
trânsito, os quais funcionam para impedir o travamento das rodas do carro
quando o sistema de freios é acionado, liberando as rodas quando estão no
limiar do deslizamento. Quando as rodas travam, a força de frenagem é governada
pelo atrito cinético.
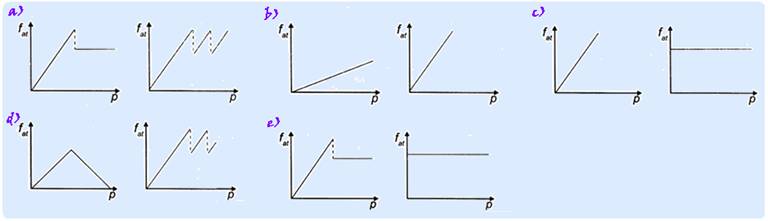
As representações esquemáticas da força de atrito fat
entre os pneus e a pista, em função da pressão p aplicada no
pedal de freio, para carros sem ABS e com ABS, respectivamente,
são
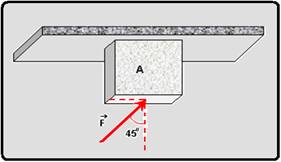
28-(UPE-PE)

Sejam os blocos P e Q de massas m e M, respectivamente,
ilustrados na figura a seguir. O coeficiente de atrito estático
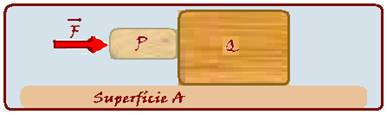
entre os blocos é μ, entretanto não existe atrito entre
o bloco Q e a superfície A. Considere g a aceleração da gravidade.
A expressão que representa o menor valor do módulo da força
horizontal 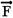 para
que o bloco P não caia, é
para
que o bloco P não caia, é

29-(UFF-RJ)

Um pano de prato retangular, com 60cm de comprimento e
constituição homogênea, está em repouso sobre uma mesa, parte sobre sua
superfície, horizontal e fina, e parte pendente, como mostra a figura.
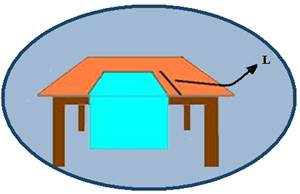
Sabendo-se que o coeficiente de atrito estático entre a superfície
da mesa e o pano é igual a 0,5 e que o pano está na iminência de
deslizar, pode-se afirmar que o comprimento L da parte sobre a mesa é:
a)
40cm
b) 20cm
c)
15cm
d)
60cm
e) 30cm
30-(ITA-SP)

Para um avião executar uma curva nivelada (sem subir ou
descer) e equilibrada, o piloto deve incliná-lo com respeito à horizontal (à
maneira de um ciclista em uma curva), de um ângulo α. Se α =
60°, a velocidade da aeronave é 100 m/s e
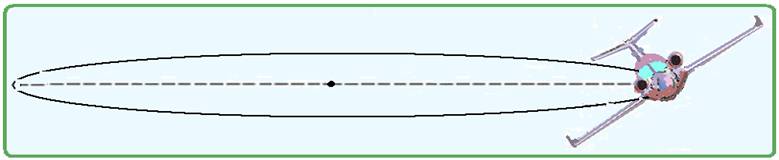
a aceleração local da gravidade é 9,5 m/s2, qual
é aproximadamente o raio de curvatura?
a) 600 m.
b) 750 m. c)
200 m.
d) 350 m.
e) 1000 m.
31-(FUVEST-SP)

Uma estação espacial, construída em forma cilíndrica, foi
projetada para contornar a ausência de gravidade no espaço. A figura mostra, de
maneira simplificada, a secção reta dessa estação, que possui dois andares.

Para simular a gravidade, a estação deve girar em torno do
seu eixo com certa velocidade angular. Se o raio externo da estação é R,
a) deduza a velocidade angular W com que a estação deve
girar para que um astronauta, em repouso no primeiro andar e a uma distância R
do eixo da estação, fique sujeito a uma aceleração igual a g.
b) Suponha que o astronauta vá para o segundo andar, a uma
distância h do piso do andar anterior. Calcule o peso do astronauta nessa
posição e compare com o seu peso quando estava no primeiro andar. O peso
aumenta, diminui ou permanece inalterado ?
32-(UFOP-MG)

Uma estação espacial é projetada como sendo um cilindro de
raio r, que gira em seu eixo com velocidade angular constante W, de modo a
produzir uma sensação de gravidade de 1g = 9,8 m/s2 nos pés de
uma pessoa que está no
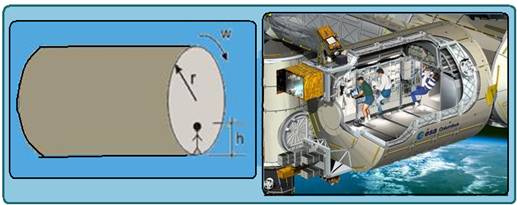
interior da estação. Admitindo-se que os seus
habitantes têm uma altura média de h = 2 m, qual deve ser o raio mínimo r
da estação, de modo que a variação da gravidade sentida entre os pés e a
cabeça
seja inferior a 1% de g?
33-(UFPE-PE)

Um bloco A de massa igual a 1kg é
mantido em repouso, em contato com o teto de um apartamento, sob o efeito de
uma força 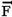 de intensidade F=20N como
ilustrado na figura a seguir. Sabendo-se que
de intensidade F=20N como
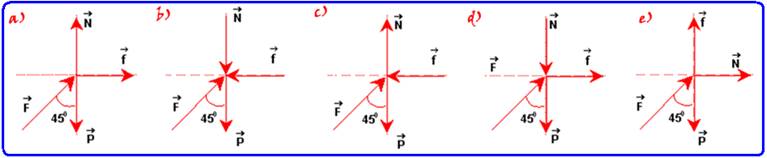
ilustrado na figura a seguir. Sabendo-se que  é a força de reação normal à
é a força de reação normal à
superfície do teto,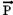 é o peso do bloco, e
é o peso do bloco, e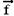 é a força de atrito, qual o
diagrama das forças que atuam sobre o bloco A?
é a força de atrito, qual o
diagrama das forças que atuam sobre o bloco A?
34-(UFG-GO)

Nas academias de ginástica, usa-se um aparelho
chamado
pressão com pernas (leg press), que tem a função de fortalecer a
musculatura
das pernas. Este aparelho possui uma parte móvel que desliza sobre um
plano
inclinado, fazendo um ângulo de 60º com a horizontal, Uma pessoa, usando
o
aparelho, empurra a parte móvel de massa igual 100 kg e a faz mover ao
longo do plano, com velocidade constante como é mostrado na figura.
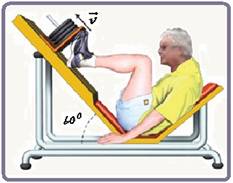
Considere o coeficiente de atrito dinâmico entre o plano inclinado e a parte móvel 0,10 e a aceleração da gravitacional 10m/s². (Usar sen60º=0,86 e cos60º=0,50).
a) Faça o diagrama das forças que estão atuando sobre a parte móvel do aparelho identificando-as.
b) Determine a intensidade da força que pessoa está aplicando sobre a parte móvel do aparelho.

Considere o coeficiente de atrito dinâmico entre o plano inclinado e a parte móvel 0,10 e a aceleração da gravitacional 10m/s². (Usar sen60º=0,86 e cos60º=0,50).
a) Faça o diagrama das forças que estão atuando sobre a parte móvel do aparelho identificando-as.
b) Determine a intensidade da força que pessoa está aplicando sobre a parte móvel do aparelho.
35-(FISICAEVESTIBULAR)

A figura abaixo mostra um carrinho de brinquedo se deslocando
com aceleração constante de 6,0 m/s2 numa superfície plana e
horizontal.
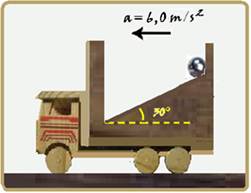
A esfera E possui massa de 1 kg e não existe atrito entre ela e o plano inclinado no qual ela está apoiada. Considere sen30o=0,5,
cos30o=0,87 e g=10m/s2. Considere a esfera E em repouso
em relação ao carrinho e determine a intensidade da força horizontal que a
parede vertical do carrinho exerce sobre a esfera.
36-(UFV/MG)

Um objeto de massa m repousa sobre um bloco de massa M, que
é empurrado contra uma parede por uma força horizontal 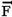 ,conforme mostra a figura abaixo.
,conforme mostra a figura abaixo.
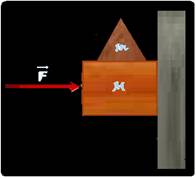
O coeficiente de atrito estático entre o bloco e a parede é
μ e o módulo da aceleração da gravidade é g. Estando o sistema em equilíbrio,
é CORRETO afirmar que o módulo da força 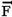 é
é

Nenhum comentário:
Postar um comentário