-
Questão 1
Prove que a bissetriz dos quadrantes ímpares é perpendicular à bissetriz dos quadrantes pares.
-
Questão 2
Considere no plano cartesiano uma reta r de equação 3x + 5y +1 =0 e um
ponto Q de coordenadas (5,5). Determine a equação da resta s
perpendicular a r passando por Q.
-
Questão 3
Prove que as retas s: x + 2y – 1 = 0 e r: 4x – 2y +12 = 0 são perpendiculares.
-
Questão 4
Encontre a equação da reta s, perpendicular à reta t: 2x + 3y – 4 =0, sabendo que ela passa pelo ponto P(3,4).
-
Questão 5
Encontre a equação da reta t que passa pelo ponto X(-1,8) e é perpendicular à bissetriz dos quadrantes ímpares.

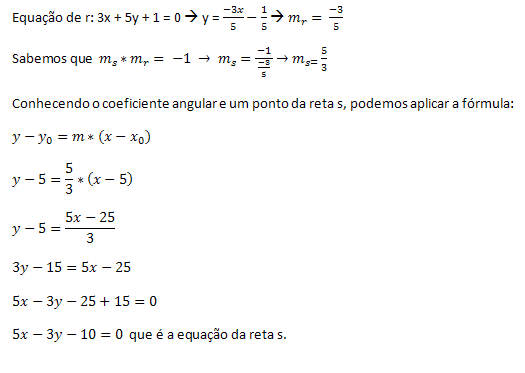



Nenhum comentário:
Postar um comentário